Python で勾配降下法を使って線形の単回帰分析をしてみた。
はじめに
Siraj Ravel さんの新しい動画シリーズ, “The Math of Intelligence"が始まった。
機械学習のための数学を毎週カバーしていくようだ。シラバスは以下。
数学に苦手意識があるので、おもしろそうなトピックだけ Coding Challenge に取り組んでいこうと思う。
Coding Challenge
初めのトピックは Gradient Descent(勾配降下法)。
昔、勉強したのだけれども、すっかり忘れていた。以下の本がとても今回役に立った。
Coding Challenge は Kaggle のデータで、勾配降下法を使って線形の単回帰分析をすること。
今回 チャレンジした Jupyter Notebook は以下です。
データセット
Kaggle のデータを使うようにとのことなので、入門用のデータセット, House Prices を使っていこうと思う。
とりあえずいちばん簡単な方法を試したいので、家の面積と価格の相関関係に注目することにした。
- SalePrice - the property’s sale price in dollars. This is the target variable that you’re trying to predict
- GrLivArea: Above grade (ground) living area square feet
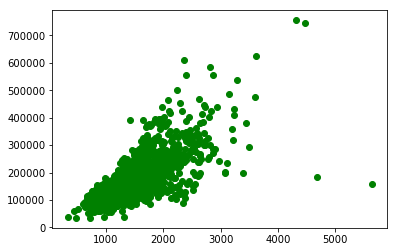
データをプロットしてみると正の相関関係がありそうなので、直線が引けそう。
勾配降下法
本当は、偏微分の数式とか書きたいけれど、数式の書き方がよくわからなかった orz
というわけで、説明抜きでいきなりコードですみません m(._.)m
参考リンクだけはっておきます。この記事のコードを参考にしました。
def calcurate_mean_squared_error(x, y, b, m):
total_error = 0
n = y.size
for i in range(n):
prediction = m*x[i] + b
total_error += (y[i] - prediction)**2
return (1/n) * total_error
def step_gradient(x, y, b, m, learning_rate):
m_grad = 0
b_grad = 0
n = y.size
#Computes the gradients
for i in range(n):
# Partial derivative for m
m_grad += -(2/n) * x[i] * (y[i] - ((m*x[i]) + b))
# Partial derivative for b
b_grad += -(2/n) * (y[i] - (m*x[i]) + b)
# update m and b
m = m - (learning_rate * m_grad)
b = b - (learning_rate * b_grad)
return b, m
def gradient_descent_runner(x, y, initial_b, initial_m, learning_rate, num_iterations):
b = initial_b
m = initial_m
past_errors = []
for i in range(num_iterations):
b, m = step_gradient(x, y, b, m, learning_rate)
if(i % 100) == 0:
error = calcurate_mean_squared_error(x, y, b, m)
past_errors.append(error)
print('Error after', i, 'iterations:', error)
return b, m, past_errors
実験結果
学習率 0.0001 だと収束しなかった。
おかしい。もっともっと学習率を小さくしても収束しない。はじめはバグっているのかと思ったけど、そうではなさそうだ。
num_iterations = 1000
learning_late = 0.0001
print("Starting gradient descent at b = {0}, m = {1}, error = {2}".format(
initial_b, initial_m,
calcurate_mean_squared_error(x, y, initial_b, initial_m)))
print("Running...")
[b, m, errors] = gradient_descent_runner(x, y, initial_b,
initial_m, learning_late, num_iterations)
print("After {0} iterations b = {1}, m = {2}, error = {3}".format(
num_iterations, b, m, calcurate_mean_squared_error(x, y, b, m)))
Starting gradient descent at b = 0, m = 1.0, error = 38434358058.74041
Running...
Error after 0 iterations: 9.29730669048e+15
/home/tsu-nera/anaconda3/envs/dlnd/lib/python3.6/site-packages/ipykernel_launcher.py:6: RuntimeWarning: overflow encountered in double_scalars
/home/tsu-nera/anaconda3/envs/dlnd/lib/python3.6/site-packages/ipykernel_launcher.py:9: RuntimeWarning: overflow encountered in double_scalars
if __name__ == '__main__':
/home/tsu-nera/anaconda3/envs/dlnd/lib/python3.6/site-packages/ipykernel_launcher.py:14: RuntimeWarning: invalid value encountered in double_scalars
Error after 100 iterations: inf
Error after 200 iterations: nan
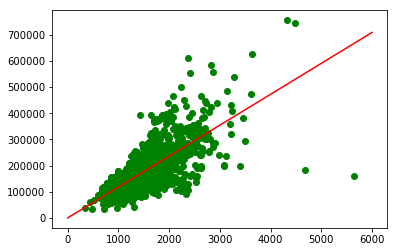
いろいろ学習率をいじって試した結果、0.000000385 というよくわからない数が最も適切だった。なんだこりゃ?!
標準化をためす
coursera の Machine Learning で、フィーチャースケーリング を習ったことを思い出した。
講座の動画を見返したら多変数の場合を扱っていた。
説明変数が1つでも、有効なのかな?とりあえず、標準化を試してみた。
norm_x = (x - x.mean()) / x.std()
今回は、学習率 0.0001 という、馴染みの値で収束した。うまくいったようだ。
コスト関数の値も plot した。イテレーションを繰り返すごとに減っている。